Packing Spheres on a Spherical Surface:
New Solution to a 100-year-old Problem

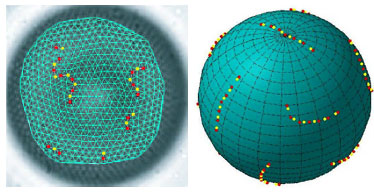
Comparison of experiment (left) and theory (right) for "scars."

Particles packed onto a flat surface organize themselves into hexagonal layer, like billiard balls before a game. The same particles packed onto a spherical surface must have at least 12 defects, as first shown by a theorem of Euler, and as experienced directly by looking at a soccer ball, which has 12 pentagons among all the remaining hexagons that make up the coating of the ball. However, the nature of the packing of particles onto larger spherical surfaces has eluded solution since the problem was first posed by J.J. Thomson nearly a century ago, and it remains one of the great unsolved problems of mathematics of the twenty first century. By studying the structure of repulsive colloidal particles on a spherical surface, Nelson, Weitz, and co-workers have shown that the pattern of defects for large spheres forms linear scars of defects, which are analogous to grain boundaries, except that they end in the middle of crystalline region, since they exist on a spherical surface. This is first experimental study of such packing, and the results are in excellent agreement with the theoretical predictions.

Such packings are observed in nature; for example the surface of viruses contain capsids, spherical objects packed onto the surface of a sphere. This work may help determine the packing of such capsids for very large viruses.

This work was featured as a highlight on the NSF website.

This work was also discussed in the News Scan section of May 2003 issue of Scientific American (p. 33).

Reference: "Grain Boundary Scars and Spherical Crystallography," A.R. Bausch, M.J. Bowick, A. Cacciuto, A. D. Dinsmore, M. F. Hsu, D. R. Nelson, M. G. Nikolaides, A. Travesset, D. A. Weitz, Science, 299, 1716 (2003).